Identified Assassins (4 Points)

Identified Assassins

We've just captured $n$ superb assassins and want to consign them to an infinite grid so they can no longer hurt anyone.

However, we also want to protect the assassins from each other! So we need to be careful where to place them in the grid.

The particular grid we've chosen has walls at every integer row/column, however it also has 6 teleporters within each cell:

• 2 of the teleporters go to cells $+x$ and $-x$ positions away horizontally
• 2 of the teleporters go to the cells $+y$ and $-y$ positions away vertically
• The final two teleporters go to cells $+a$ horizontally and $+b$ cells vertically, or $-a$ horizontally and $-b$ cells vertically

For example, for a configuration of $x=3$, $y=2$, $a=1$, $b=4$, there are 6 distinct locations the teleporters can take you:

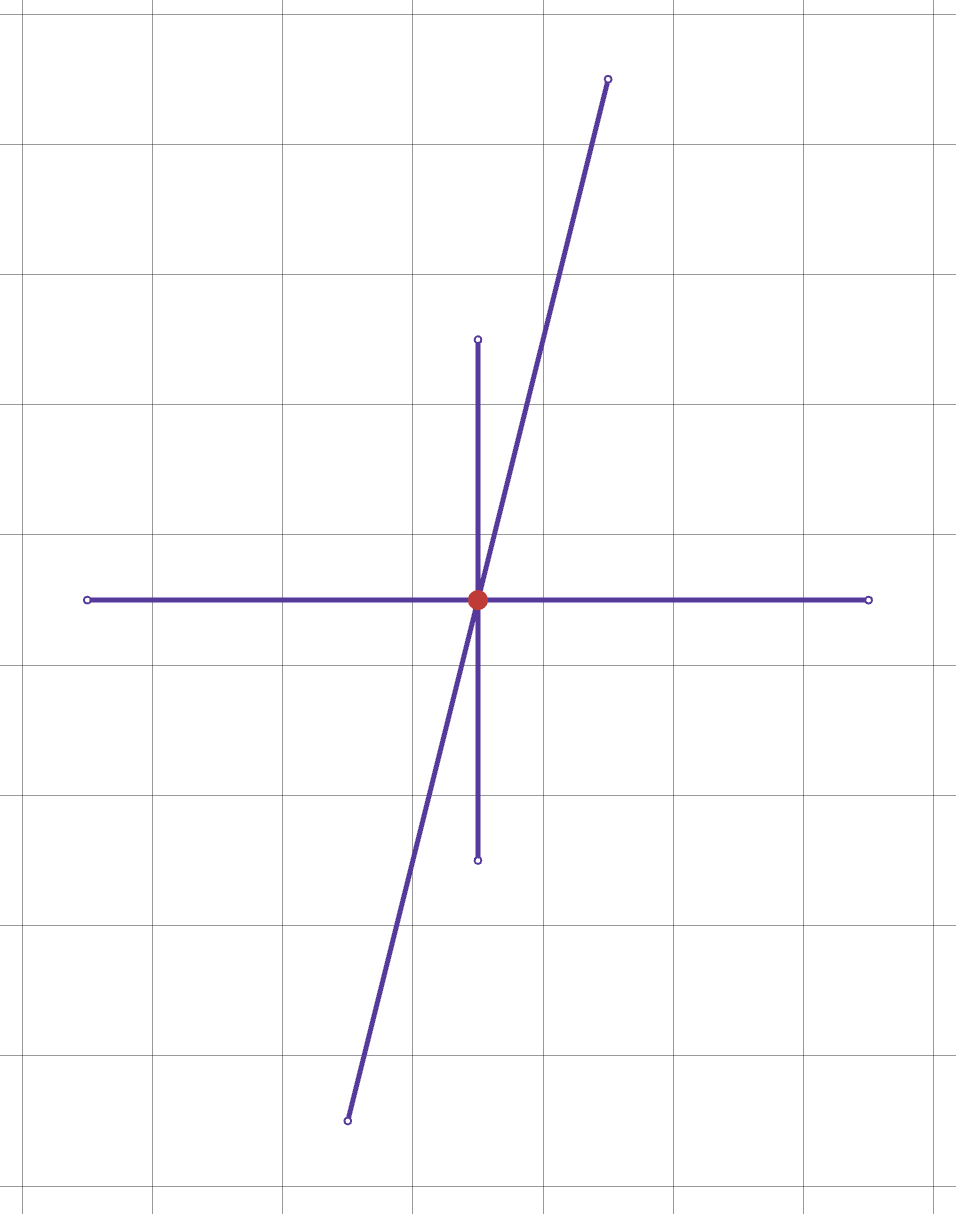
Given we have $n$ assassins, and if there is some way for assassins to meet, they will eventually find each other, if placed randomly what are the chances all $n$ assassins are isolated?

Input

Input will be a single line containing 5 space-separated integers, $n, x, y, a, b$.

Output

Output should be a single integer. Since the numbers can be rather large, output will use modular inverse.

Let $\frac{p}{q}$ be the probability that all $n$ assassins are isolated, then output $p \times q^{-1}$ modulo $m$, where $q^{-1}$ is the modular inverse of $q$ with respect to $m = 10^9+7$.

Constraints

• $1 \leq n \leq 25$
• $0 \leq x, y, a, b \leq 10^9$

Example 1

For Input

3 3 2 1 4

The output should be 0, seeing as there is a $\frac{0}{1}$ chance that the 3 assassins would be isolated.

Example 2

For Input

2 3 2 1 4

The output should be 500000004, seeing as there is a $\frac{1}{2}$ chance that the 2 assassins would be isolated, and the modular inverse of $2$ w.r.t. $10^9+7$ is $500000004$.

Example 3

For Input 4 0 10 1 5

The output should be 928000007, seeing as there is a $\frac{63}{125}$ chance that the 4 assassins would be isolated, and the modular inverse of $125$ w.r.t. $10^9+7$ is $928000007$. (And $24 \times 928000007$ is congruent with $928000007$ mod $10^9+7$)

Some starter code

Just in-case you need it, you can do modular arithmetic in Python with the following tools:

MOD = 10 ** 9 + 7

z = a % MOD # Modulo MOD

def modinv(a, m=MOD):
    # Returns the modular inverse if a, mod m. Assumes a and m are coprime.
    # This could also just be `pow(a, -1, m)`
    m0, x0, x1 = m, 0, 1
    while a > 1:
        q = a // m
        m, a = a % m, m
        x0, x1 = x1 - q * x0, x0
    return x1 + m0 if x1 < 0 else x1

# (a^b) % m
z = pow(a, b, m)